Tiedolla johtamisessa yritykset hyödyntävät informaatiota päätöksenteon tukena. Nykyaikaisen teknologian ansiosta uutta tietoa on käytettävissä entistä enemmän, mutta samalla kasvava tiedon määrä tekee sen hyödyntämisestä entistä vaikeampaa. Suurten tietomassojen hyödyntäminen vaatii tuekseen erilaisia menetelmiä, joiden avulla datasta löydetään uutta informaatiota ja tunnistetaan päätöksenteon kannalta oleelliset muuttujat.

Erola ja Lehikoinen (2021) käsittelivät opinnäytetyössään Kaukolämpötuotannon optimointi, raportointi ja visualisointi Saas-palveluna kaukolämmön tuotannon optimointia. Tavoitteena oli selvittää kannattavuuden suhteen optimaalisin tapa tuottaa kaukolämpötehoa. Työssä vertailtiin matemaattisen optimoinnin ja koneoppimisen menetelmien käyttökelpoisuutta optimointiongelman ratkaisemiseksi. (Erola & Lehikoinen 2021.) Kaukolämmön tuotannon kannattavuuteen vaikuttavia tekijöitä on useita, kuten polttoaineiden energiasisältö ja hinta, tuotannon hävikki ja päästöistä aiheutuvat kulut (Neittaanmäki & Schroderus 2010, 4). Ennen optimointimallin rakentamista valitaan kannattavuuteen eniten vaikuttavat tekijät tilastollisen analyysin perusteella.
Matemaattinen optimointi ratkaisee ongelman
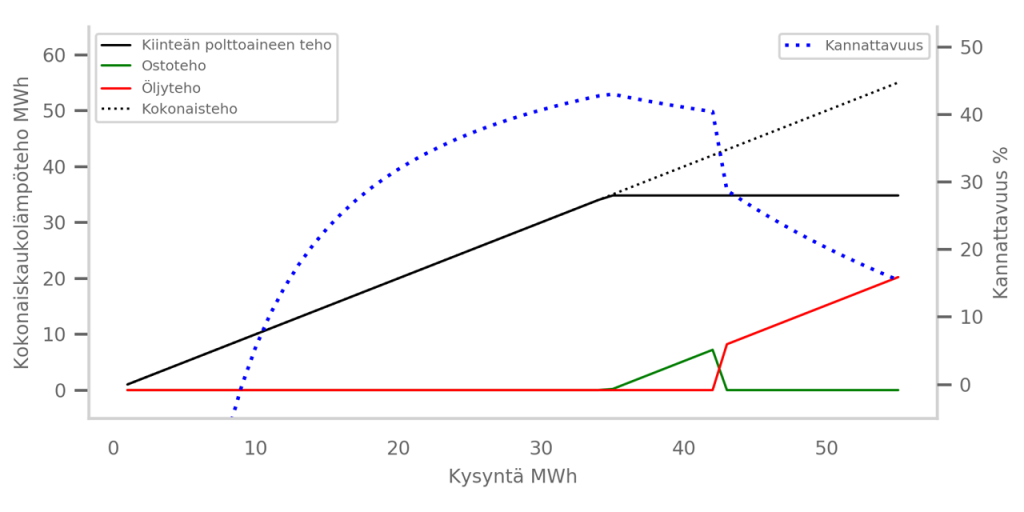
Matemaattisen optimoinnin menetelmillä voidaan ratkaista moninaisia ongelmia, kuten etsiä ratkaisuja kulujen pienentämiseksi tai tuotannon lisäämiseksi kannattavasti. Todellinen ongelma kuvataan matemaattisella mallilla. Malli esittää ongelmaan liittyvät muuttujat, rajoitteet sekä kohdefunktion, joka toimii tavoitellun lopputuloksen mittarina. Mittarina voi olla erilaisia liiketoiminnallisia numeerisia tavoitteita. (Nocedal & Wright, 2.) Kaukolämmön tuotannon kannattavuuden optimoinnissa matemaattisen optimoinnin avulla löydettiin tuotantomuotojen optimaalisin yhdistelmä, joka täyttää lämpöenergian kysynnän ja maksimoi kannattavuuden.
Koneoppimisen menetelmillä lisäarvoa datasta
Koneoppimisessa dataa käytetään erilaisten ennustemallien luomiseen. Malli kykenee kuvailemaan datamassoja opetusaineiston perusteella ja tekemään dataan perustuvia ennusteita, joita voidaan hyödyntää päätöksenteossa mm. ennakoimalla tulevia tapahtumia. (Géron 2017, 6–7.) Kaukolämmön tuotannon optimaalisinta kombinaatiota tutkittiin myös koneoppimisen menetelmillä historiadatan avulla. Koneoppimisen menetelmiä voidaan soveltaa kaukolämmön tuotannon optimoinnissa, mutta lopputulos riippuu täysin datasta. Malli yleistää sille syötetyn datan, joten se ei välttämättä tuota optimaalisinta tulosta. Koneoppimisen menetelmiä hyödyntäen saatiin kuitenkin kokonaiskuva kaukolämmön tuotannon nykytilanteesta.
Yhteenveto
Matemaattisen optimoinnin menetelmät soveltuvat hyvin optimointiongelmien ratkaisemiseen, mutta koneoppiminen ei välttämättä sellaisenaan tuo lisäarvoa. Koneoppimisen menetelmillä voidaan kuitenkin löytää olemassa olevasta datasta informaatiota, jota voidaan käyttää matemaattisen optimoinnin parametreina paremman ratkaisun löytämiseksi.
Kirjoittajat
Lehtori Minna Asplund, TkL, toimii koordinaattorina insinööri YAMK-tutkinnon digitaaliset ratkaisut -koulutuksessa.
Jarmo Erola opiskeli LAB-ammattikorkeakoulussa insinööri YAMK-tutkinnon digitaaliset ratkaisut -koulutuksessa ja työskentelee ohjelmistokehittäjänä muun muassa koneoppimisen parissa. Artikkeli perustuu Erolan ja Antti Lehikoisen yhteistyössä tekemäänsä opinnäytetyöhön.
Lähteet
Erola, J. & Lehikoinen, A. 2021. Kaukolämpötuotannon optimointi, raportointi ja visualisointi Saas-palveluna. Opinnäytetyö YAMK. LAB-ammattikorkeakoulu. [Viitattu 6.6.2021]. Saatavissa:
http://urn.fi/URN:NBN:fi:amk-2021060314064
Géron, A. 2017. Hands-On Machine Learning with Scikit-Learn & TensorFlow – Concepts, Tools, and Techniques to Build Intelligent Systems. Sebastopol: O’Reilly Media Inc.
Neittaanmäki, P. & Schroderus, O. 2010. Sähkön- ja lämmöntuotannon kustannussimulointi ja herkkyysanalyysi. [Viitattu 2.5.2021]. Saatavissa
http://www.mit.jyu.fi/scoma/energiasimulaattori/energiasimulointi_140610.pdf
Nocedal, J. & Wright, S. 2006. Numerical Optimization. 2. painos. New York: Springer.
Linkit
Linkki 1. Erola, J. & Lehikoinen, A. 2021. Kaukolämpötuotannon optimointi, raportointi ja visualisointi Saas-palveluna. Opinnäytetyö YAMK. LAB-ammattikorkeakoulu. [Viitattu 6.6.2021]. Saatavissa:
http://urn.fi/URN:NBN:fi:amk-2021060314064
Kuvat
Kuva 1. Ku, K. 2017. Black Farmed Eyeglasses in Front of Laptop Computer. Pexels. [Viitattu 6.6.2021]. Saatavissa:
https://www.pexels.com/photo/black-farmed-eyeglasses-in-front-of-laptop-computer-577585/
Kuva 2. Erola, J. & Lehikoinen, A. 2021. Lineaarisella optimoinnilla selvitetyt optimaaliset tuotantokombinaatiot kysynnän suhteen. Teoksessa: Erola, J. & Lehikoinen, A. 2021. Kaukolämpötuotannon optimointi, raportointi ja visualisointi Saas-palveluna. 41.